संख्या प्रणाली प्रतीकों और नियमों के एक सेट की सहायता से संख्या रेखा पर संख्याओं का प्रतिनिधित्व करने की एक विधि है। ये प्रतीक 0-9 तक होते हैं और इन्हें अंक कहा जाता है। संख्या प्रणाली का उपयोग गणितीय गणनाओं को करने के लिए किया जाता है जिसमें महान वैज्ञानिक गणनाओं से लेकर गणनाओं तक की गणना होती है जैसे कि बच्चे के लिए खिलौनों की संख्या या बॉक्स में शेष चॉकलेट की संख्या की गणना करना। नंबर सिस्टम में इसके अंकों के आधार मान के आधार पर कई प्रकार होते हैं।
संख्या प्रणाली या अंक प्रणाली संख्याओं के नामकरण या प्रतिनिधित्व की प्रणाली है। गणित में विभिन्न प्रकार की संख्या प्रणालियाँ हैं जैसे बाइनरी, दशमलव, आदि। इस पाठ में अंक प्रणाली की संपूर्ण अवधारणाओं को उनके प्रकार, रूपांतरण और प्रश्नों के साथ शामिल किया गया है।
What is Number System in Maths?
एक संख्या प्रणाली को संख्याओं को व्यक्त करने के लिए लिखने की प्रणाली के रूप में परिभाषित किया गया है। यह अंकों या अन्य प्रतीकों का एक सुसंगत तरीके से उपयोग करके किसी दिए गए सेट की संख्याओं का प्रतिनिधित्व करने के लिए गणितीय संकेतन है। यह प्रत्येक संख्या का एक अनूठा प्रतिनिधित्व प्रदान करता है और अंकों की अंकगणितीय और बीजगणितीय संरचना का प्रतिनिधित्व करता है। यह हमें जोड़, घटाव और भाग जैसे अंकगणितीय कार्यों को संचालित करने की भी अनुमति देता है।
किसी संख्या में किसी भी अंक का मान निम्न द्वारा निर्धारित किया जा सकता है:
- अंक
- संख्या में इसकी स्थिति
- संख्या प्रणाली का आधार
What is Number?
Types of Number System
- दशमलव संख्या प्रणाली (आधार- 10)Decimal Number System
- बाइनरी नंबर सिस्टम (आधार- 2)Binary Number System
- अष्टक संख्या प्रणाली (आधार-8)Octal Number System
- हेक्साडेसिमल संख्या प्रणाली (आधार- 16)Hexadecimal Number System
Decimal Number System (Base 10 Number System)
दशमलव संख्या प्रणाली में 10 अंक 0, 1, 2, 3, 4, 5, 6, 7, 8 और 9 होते हैं और यह सबसे अधिक इस्तेमाल की जाने वाली संख्या प्रणाली है। हम इन 10 अंकों के संयोजन का उपयोग अन्य सभी संख्याओं को बनाने के लिए करते हैं। किसी संख्या में अंक का मान संख्या में उसके स्थान पर निर्भर करता है। दशमलव संख्या प्रणाली के लिए स्थानीय मान तालिका इस प्रकार है:

बायीं ओर का प्रत्येक स्थान अपने दायीं ओर के स्थान से दस गुना बड़ा होता है, अर्थात जैसे-जैसे हम दायें से बायें जाते हैं, प्रत्येक स्थान के साथ स्थानीय मान दस गुना बढ़ जाता है।

एक दशमलव संख्या प्रणाली को आधार 10 प्रणाली भी कहा जाता है।
एक संख्या 49,365 को उनतालीस हजार तीन सौ पैंसठ के रूप में पढ़ा जाता है, जहां 4 का मान चालीस हजार, 9 का नौ हजार, 3 का तीन सौ, 6 का साठ और 5 का पांच होता है।
Binary Number System (Base 2 Number System)
बाइनरी नंबर सिस्टम में, हम केवल दो अंक 0 और 1 का उपयोग करते हैं। इसका मतलब है कि 2 नंबर सिस्टम।
बाइनरी नंबरों का उदाहरण: १०११; १०१०१०; ११०११०१

बाइनरी नंबर के प्रत्येक अंक को बिट कहा जाता है। तो, एक बाइनरी नंबर 101 में 3 बिट होते हैं। 499787080
कंप्यूटर और अन्य डिजिटल डिवाइस बाइनरी सिस्टम का उपयोग करते हैं। बाइनरी नंबर सिस्टम बेस 2 का उपयोग करता है।
Example
(14)10 को एक द्विआधारी संख्या के रूप में लिखिए।
Solution:

Base 2 Number System Example
∴ (14)10 = 11102
Octal Number System (Base 8 Number System)
Example: Convert 2158 into decimal.
Solution:
2158 = 2 × 82 + 1 × 81 + 5 × 80
= 2 × 64 + 1 × 8 + 5 × 1
= 128 + 8 + 5
= 14110
Hexadecimal Number System (Base 16 Number System)
| Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
नीचे दी गई तालिका दशमलव, बाइनरी और हेक्साडेसिमल संख्याओं का उपयोग करके संख्या 1 से 20 दिखाती है।
Decimal | Binary | Hexadecimal |
0 | 0 | 0 |
1 | 1 | 1 |
2 | 10 | 2 |
3 | 11 | 3 |
4 | 100 | 4 |
5 | 101 | 5 |
6 | 110 | 6 |
7 | 111 | 7 |
8 | 1000 | 8 |
9 | 1001 | 9 |
10 | 1010 | 10 |
11 | 1011 | A |
12 | 1100 | B |
13 | 1101 | C |
14 | 1110 | D |
15 | 1111 | E |
16 | 10000 | F |
17 | 10001 | 11 |
18 | 10010 | 12 |
19 | 10011 | 13 |
20 | 10100 | 14 |
Fun Facts
दशमलव संख्या प्रणाली को हिंदू-अरबी अंक प्रणाली भी कहा जाता है।
मानवविज्ञानी परिकल्पना करते हैं कि दशमलव प्रणाली सबसे अधिक इस्तेमाल की जाने वाली संख्या प्रणाली थी, क्योंकि मनुष्यों के प्रत्येक हाथ में पांच उंगलियां और दोनों में दस उंगलियां होती हैं।
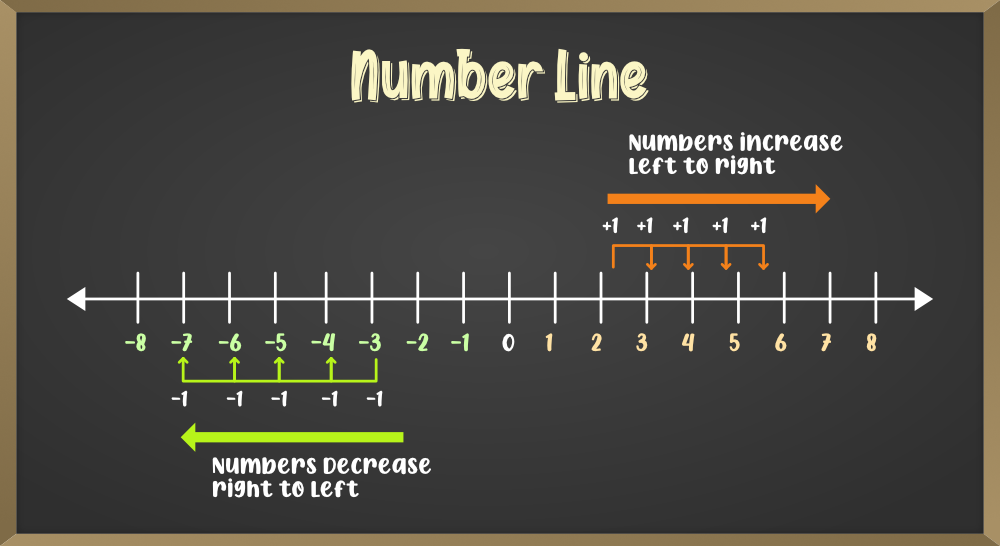
एक संख्या रेखा एक सीधी रेखा पर बीच में एक निश्चित अंतराल के साथ संख्याओं का प्रतिनिधित्व करती है। एक संख्या रेखा में सभी प्रकार की संख्याएँ होती हैं जैसे प्राकृत संख्याएँ, परिमेय, पूर्णांक आदि। संख्या रेखा पर संख्याएँ बाएँ से दाएँ जाने पर बढ़ती हैं और दाएँ से बाएँ जाने पर घटती हैं। एक संख्या रेखा के सिरों को परिभाषित नहीं किया जाता है अर्थात, एक संख्या रेखा पर संख्याएँ शून्य के बाईं ओर अनंत से लेकर शून्य के दाईं ओर अनंत तक होती हैं।
धनात्मक संख्याएँ: वे संख्याएँ जो शून्य के दाईं ओर निरूपित होती हैं, धनात्मक संख्याएँ कहलाती हैं। इन संख्याओं का मान दायीं ओर बढ़ने पर बढ़ता है। संख्याओं के बीच जोड़ने के लिए धनात्मक संख्याओं का उपयोग किया जाता है। उदाहरण: १, २, ३, ४,…
Conversion of Number Systems
1. Conversion from Decimal Number System to Other Number Systems
दशमलव संख्याओं को अंक 0-9 और आधार 10 के साथ दर्शाया जाता है। एक संख्या प्रणाली के रूपांतरण का अर्थ है एक आधार से दूसरे आधार में रूपांतरण। दशमलव संख्या प्रणाली का अन्य संख्या प्रणालियों में रूपांतरण निम्नलिखित है:
A. Decimal to Binary Conversion:
दशमलव संख्याओं को आधार १० में दर्शाया जाता है, लेकिन द्विआधारी संख्याएँ आधार २ की होती हैं। इसलिए, दशमलव संख्या को द्विआधारी संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होता है। नीचे दिए गए चरणों का पालन करें:
चरण 1: दशमलव संख्या को उस संख्या प्रणाली के आधार से विभाजित करें जिसमें परिवर्तित किया जाना है। यहाँ रूपांतरण बाइनरी में है, इसलिए भाजक 2 होगा।
चरण 2: भाग से प्राप्त शेष नई संख्या का सबसे छोटा सार्थक अंक बन जाएगा।
चरण 3: भाग से प्राप्त भागफल अगला लाभांश बन जाएगा और आधार अर्थात 2 से विभाजित हो जाएगा।
चरण 4: प्राप्त शेष दूसरा सबसे छोटा सार्थक अंक बन जाएगा अर्थात इसे पहले प्राप्त अंक के बाईं ओर जोड़ा जाएगा।
अब, चरण 3 और 4 को तब तक दोहराया जाता है जब तक कि प्राप्त भागफल 0 नहीं हो जाता है, और प्रत्येक पुनरावृत्ति के बाद प्राप्त शेष को मौजूदा अंकों के बाईं ओर जोड़ दिया जाता है।
सभी पुनरावृत्तियों के समाप्त होने के बाद, अंतिम प्राप्त शेष को सबसे महत्वपूर्ण अंक कहा जाएगा।
B. Decimal to Octal Conversion:
अष्टक संख्याओं को आधार 8 में दर्शाया जाता है। इसलिए किसी दशमलव संख्या को अष्टक संख्या में बदलने के लिए उस संख्या के आधार को बदलना होता है। नीचे दिए गए चरणों का पालन करें:
चरण 1: दशमलव संख्या को उस संख्या प्रणाली के आधार से विभाजित करें जिसमें परिवर्तित किया जाना है। यहां रूपांतरण अष्टाधारी है, इसलिए भाजक 8 होगा।
चरण 2: भाग से प्राप्त शेष नई संख्या का सबसे छोटा सार्थक अंक बन जाएगा।
चरण 3: भाग से प्राप्त भागफल अगला लाभांश बन जाएगा और इसे आधार अर्थात 8 से विभाजित किया जाएगा।
चरण 4: प्राप्त शेष दूसरा सबसे छोटा सार्थक अंक बन जाएगा अर्थात इसे पहले प्राप्त अंक के बाईं ओर जोड़ दिया जाएगा।
अब, चरण ३ और ४ को तब तक दोहराया जाता है जब तक कि प्राप्त भागफल ० नहीं हो जाता है, और प्रत्येक पुनरावृत्ति के बाद प्राप्त शेष को मौजूदा अंकों के बाईं ओर जोड़ दिया जाता है।
C. Decimal to Hexadecimal Conversion:
हेक्साडेसिमल संख्याओं को आधार 16 में दर्शाया जाता है। इसलिए, दशमलव संख्या को हेक्साडेसिमल संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होगा। नीचे दिए गए चरणों का पालन करें:
चरण 1: दशमलव संख्या को उस संख्या प्रणाली के आधार से विभाजित करें जिसमें परिवर्तित किया जाना है। यहां रूपांतरण हेक्स में है इसलिए भाजक 16 होगा।
चरण 2: भाग से प्राप्त शेष नई संख्या का सबसे छोटा सार्थक अंक बन जाएगा।
चरण 3: भाग से प्राप्त भागफल अगला लाभांश बन जाएगा और आधार अर्थात 16 से विभाजित हो जाएगा।
चरण 4: प्राप्त शेष दूसरा सबसे छोटा सार्थक अंक बन जाएगा अर्थात इसे पहले प्राप्त अंक के बाईं ओर जोड़ दिया जाएगा।
अब, चरण ३ और ४ को तब तक दोहराया जाता है जब तक कि प्राप्त भागफल ० नहीं हो जाता है, और प्रत्येक पुनरावृत्ति के बाद प्राप्त शेष को मौजूदा अंकों के बाईं ओर जोड़ दिया जाता है।
2. Conversion from Binary Number System to Other Number Systems
बाइनरी नंबरों को अंक 0 और 1 और आधार 2 के साथ दर्शाया जाता है। एक संख्या प्रणाली के रूपांतरण का अर्थ है एक आधार से दूसरे आधार में रूपांतरण। बाइनरी नंबर सिस्टम का अन्य नंबर सिस्टम में रूपांतरण निम्नलिखित है:
A. Binary to Decimal Conversion:
बाइनरी नंबरों को आधार 2 में दर्शाया जाता है लेकिन दशमलव संख्याएं आधार 10 की होती हैं। इसलिए, बाइनरी संख्या को दशमलव संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होता है। नीचे दिए गए चरणों का पालन करें:
चरण 1: बाइनरी नंबर के प्रत्येक अंक को उस अंक के स्थानीय मान से गुणा करें, जो दाएं से बाएं यानी एलएसबी से एमएसबी तक शुरू होता है।
चरण 2: इस गुणन के परिणाम को जोड़ें और दशमलव संख्या बन जाएगी।
उदाहरण: (11101011)2 को दशमलव संख्या में बदलने के लिए
B. Binary to Octal Conversion:
Binary numbers are represented in base 2 but the octal numbers are of base 8. Hence, to convert the binary number into octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the binary number into groups of three digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent octal digits.
Example: To convert (11101011)2 into an octal number
C. Binary to Hexadecimal Conversion:
बाइनरी नंबर को बेस 2 में दर्शाया जाता है लेकिन हेक्साडेसिमल नंबर बेस 10 के होते हैं। इसलिए, बाइनरी नंबर को हेक्स नंबर में बदलने के लिए, उस नंबर के बेस को बदलना होता है। नीचे दिए गए चरणों का पालन करें:
चरण 1: द्विआधारी संख्या को चार अंकों के समूहों में विभाजित करें जो दाएं से बाएं यानी एलएसबी से एमएसबी तक शुरू होते हैं।
चरण 2: इन समूहों को समकक्ष हेक्स अंकों में परिवर्तित करें।
उदाहरण: (1110101101101)2 को हेक्स नंबर में बदलने के लिए
3. Conversion from Octal Number System to Other Number Systems
अष्टक संख्याओं को अंक 0-7 और आधार 8 के साथ दर्शाया जाता है। एक संख्या प्रणाली के रूपांतरण का अर्थ है एक आधार से दूसरे आधार में रूपांतरण। ऑक्टल नंबर सिस्टम का अन्य नंबर सिस्टम में रूपांतरण निम्नलिखित हैं:
A. Octal to Decimal Conversion:
अष्टक संख्याओं को आधार 8 में दर्शाया जाता है, लेकिन दशमलव संख्याएँ आधार 10 की होती हैं। इसलिए, किसी अष्टक संख्या को दशमलव संख्या में बदलने के लिए उस संख्या के आधार को बदलना होता है। नीचे दिए गए चरणों का पालन करें:
चरण 1: ऑक्टल संख्या के प्रत्येक अंक को उस अंक के स्थानीय मान से गुणा करें, जो दाएं से बाएं यानी एलएसबी से एमएसबी तक शुरू होता है।
चरण 2: इस गुणन के परिणाम को जोड़ें और दशमलव संख्या बन जाएगी।
उदाहरण:
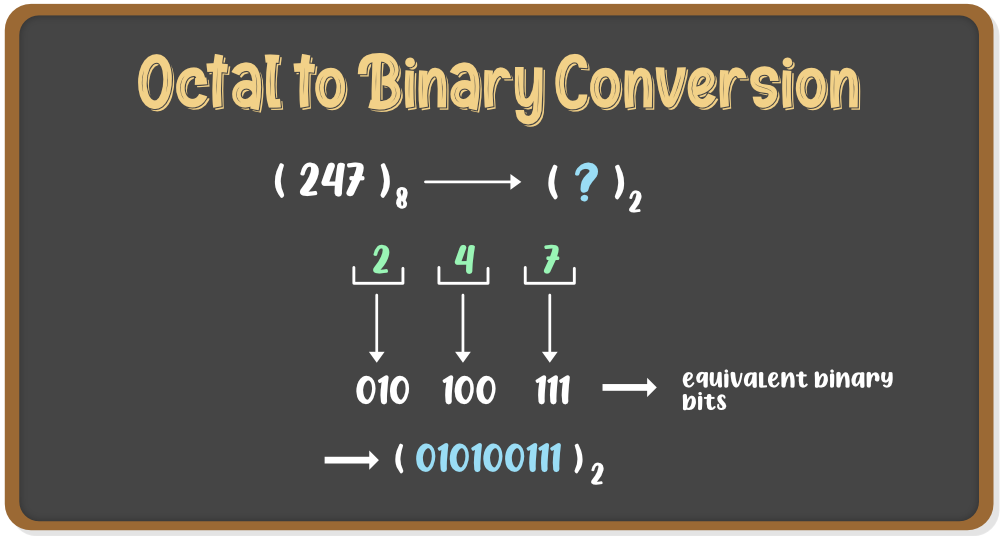
B. Octal to Binary Conversion:
अष्टक संख्याओं को आधार 8 में दर्शाया जाता है, लेकिन द्विआधारी संख्याएँ आधार 2 की होती हैं। इसलिए, एक अष्टक संख्या को एक द्विआधारी संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होता है। नीचे दिए गए चरणों का पालन करें:
चरण 1: अष्टक संख्या के प्रत्येक अंक को अलग-अलग लिखें।
चरण 2: प्रत्येक अंक को तीन बाइनरी अंकों के समकक्ष समूह में परिवर्तित करें।
चरण 3: इन समूहों को मिलाकर पूर्ण बाइनरी संख्या बनाएं।
उदाहरण: (२४७)८ को बाइनरी में बदलना है
C. Octal to Hexadecimal Conversion:
अष्टक संख्याओं को आधार 8 में दर्शाया जाता है, लेकिन हेक्साडेसिमल संख्याएँ आधार 16 की होती हैं। इसलिए, एक अष्टक संख्या को एक हेक्स संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होगा। नीचे दिए गए चरणों का पालन करें:
चरण 1: हमें पहले ऑक्टल नंबर को बाइनरी में बदलना होगा। उसके लिए, उपरोक्त रूपांतरण में दिए गए चरणों का पालन करें।
चरण 2: अब बाइनरी नंबर को हेक्स नंबर में बदलने के लिए, बाइनरी अंकों को दाएं से बाएं यानी एलएसबी से एमएसबी तक चार अंकों के समूहों में विभाजित करें।
चरण 3: MSB से पहले इसे चार अंकों का एक उचित समूह बनाने के लिए शून्य जोड़ें (यदि आवश्यक हो)
चरण 4: अब इन समूहों को उनके प्रासंगिक दशमलव मानों में परिवर्तित करें।
चरण ५: १०-१५ से मूल्यों के लिए, इसे हेक्स प्रतीकों में परिवर्तित करें यानी ए-एफ . से
उदाहरण: (५४५६)८ को हेक्स में बदलना है
4. Conversion from Hexadecimal Number System to Other Number Systems
हेक्स नंबर 0-9 अंकों के साथ और ए-एफ अक्षरों के साथ और आधार 16 के साथ दर्शाए जाते हैं। एक संख्या प्रणाली के रूपांतरण का अर्थ है एक आधार से दूसरे आधार में रूपांतरण। हेक्साडेसिमल नंबर सिस्टम का अन्य नंबर सिस्टम में रूपांतरण निम्नलिखित हैं:
A. Hexadecimal to Decimal Conversion:
हेक्साडेसिमल संख्याओं को आधार 16 में दर्शाया जाता है लेकिन दशमलव संख्याएँ आधार 10 की होती हैं। इसलिए, एक हेक्साडेसिमल संख्या को दशमलव संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होगा। नीचे दिए गए चरणों का पालन करें:
चरण 1: हेक्स संख्या में उपयोग किए गए प्रतीकों का दशमलव मान लिखिए अर्थात A-F . से
चरण 2: हेक्स संख्या के प्रत्येक अंक को उसके स्थानीय मान से गुणा करें। दाएं से बाएं यानी एलएसबी से एमएसबी तक।
चरण 3: गुणा का परिणाम जोड़ें और अंतिम योग दशमलव संख्या होगी।
उदाहरण: (8EB4)16 को दशमलव मान में बदलने के लिए
B. Hexadecimal to Binary Conversion:
हेक्स संख्याओं को आधार 16 में दर्शाया जाता है, लेकिन द्विआधारी संख्याएं आधार 2 की होती हैं। इसलिए, एक हेक्साडेसिमल संख्या को एक द्विआधारी संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होगा। नीचे दिए गए चरणों का पालन करें:
चरण 1: हेक्स प्रतीकों को इसके समकक्ष दशमलव मानों में परिवर्तित करें।
चरण 2: हेक्साडेसिमल संख्या के प्रत्येक अंक को अलग से लिखें।
चरण 3: प्रत्येक अंक को चार बाइनरी अंकों के समकक्ष समूह में परिवर्तित करें।
चरण 4: इन समूहों को मिलाकर पूर्ण बाइनरी संख्या बनाएं।
उदाहरण: (B2E)16 को बाइनरी में बदलना है
C. Hexadecimal to Octal Conversion:
हेक्साडेसिमल संख्याओं को आधार 16 में दर्शाया जाता है, लेकिन अष्टक संख्याएँ आधार 8 की होती हैं। इसलिए, एक हेक्स संख्या को एक अष्टक संख्या में बदलने के लिए, उस संख्या के आधार को बदलना होगा। नीचे दिए गए चरणों का पालन करें:
चरण 1: हमें पहले हेक्साडेसिमल संख्या को बाइनरी में बदलना होगा। उसके लिए, उपरोक्त रूपांतरण में दिए गए चरणों का पालन करें।
चरण 2: अब बाइनरी नंबर को ऑक्टल नंबर में बदलने के लिए, बाइनरी अंकों को दाएं से बाएं यानी एलएसबी से एमएसबी तक तीन अंकों के समूहों में विभाजित करें।
चरण 3: इसे तीन अंकों का एक उचित समूह बनाने के लिए MSB से पहले शून्य जोड़ें (यदि आवश्यक हो)
चरण 4: अब इन समूहों को उनके प्रासंगिक दशमलव मानों में परिवर्तित करें।
उदाहरण: (B2E)16 को hex . में बदलना है