Geometry

ज्यामिति गणित की वह शाखा है जो रोजमर्रा की जिंदगी में दिखाई देने वाली विभिन्न चीजों के आकार, कोण, आयाम और आकार से संबंधित है। यूक्लिडियन ज्यामिति में, दो-आयामी आकार और तीन-आयामी आकार होते हैं।

समतल ज्यामिति में 2 आकृतियाँ जैसे त्रिभुज, वर्ग, आयत, वृत्त भी समतल आकृतियाँ कहलाती हैं। ठोस ज्यामिति में घन, घनाभ, शंकु आदि जैसी 3d आकृतियों को ठोस भी कहा जाता है। मूल ज्यामिति बिंदु, रेखा और तल पर आधारित है, जिसे निर्देशांक ज्यामिति में समझाया गया है।

ज्यामिति में विभिन्न प्रकार की आकृतियाँ हमें दैनिक जीवन की आकृतियों को समझने में मदद करती हैं। ज्यामितीय अवधारणाओं की सहायता से, हम क्षेत्रफल, परिधि और आकृतियों के आयतन की गणना कर सकते हैं।

Branches of Geometry

(i) बीजगणितीय ज्यामिति - बहुभिन्नरूपी बहुपद के शून्यों का अध्ययन करने वाली ज्यामिति की एक शाखा है। इसमें रैखिक और बहुपद बीजीय समीकरण शामिल हैं जिनका उपयोग शून्य के सेट को हल करने के लिए किया जाता है। इस प्रकार के अनुप्रयोग में क्रिप्टोग्राफी, स्ट्रिंग सिद्धांत आदि शामिल हैं।

(ii) असतत ज्यामिति - सरल ज्यामितीय वस्तु की सापेक्ष स्थिति से संबंधित है, जैसे कि बिंदु, रेखाएं, त्रिकोण, वृत्त आदि।

(iii) डिफरेंशियल ज्योमेट्री - समस्या-समाधान के लिए बीजगणित और कलन की तकनीकों का उपयोग करता है। विभिन्न समस्याओं में भौतिकी आदि में सामान्य सापेक्षता शामिल है।

(iv) यूक्लिडियन ज्यामिति - बिंदुओं, रेखाओं, तलों, कोणों, सर्वांगसमता, समानता, ठोस आकृतियों सहित स्वयंसिद्धों और प्रमेयों पर आधारित समतल और ठोस आकृतियों का अध्ययन। इसमें कंप्यूटर विज्ञान, आधुनिक गणित समस्या समाधान, क्रिस्टलोग्राफी आदि में अनुप्रयोगों की एक विस्तृत श्रृंखला है।

(v) उत्तल ज्यामिति - वास्तविक विश्लेषण की तकनीकों का उपयोग करते हुए यूक्लिडियन अंतरिक्ष में उत्तल आकृतियाँ शामिल हैं। संख्या सिद्धांत में अनुकूलन और कार्यात्मक विश्लेषण में इसका अनुप्रयोग है।

(vi) टोपोलॉजी - निरंतर मानचित्रण के तहत अंतरिक्ष के गुणों से संबंधित है। इसके आवेदन में कॉम्पैक्टनेस, पूर्णता, निरंतरता, फिल्टर, फ़ंक्शन स्पेस, ग्रिल, क्लस्टर और बंच, हाइपरस्पेस टोपोलॉजी, प्रारंभिक और अंतिम संरचनाएं, मीट्रिक रिक्त स्थान, जाल, समीपस्थ निरंतरता, निकटता रिक्त स्थान, पृथक्करण स्वयंसिद्ध और समान रिक्त स्थान शामिल हैं।

Geometry Formulas

विभिन्न ज्यामितीय आकृतियों की लंबाई, चौड़ाई और ऊंचाई का उपयोग करके क्षेत्रफल, परिधि, आयतन और विभिन्न मापों की गणना करने के लिए, ज्यामिति सूत्र महत्वपूर्ण हैं। सूत्रों का उपयोग करके, हम आसानी से उपायों की गणना कर सकते हैं। ज्यामिति में सीखने के लिए बहुत सारे सूत्र हैं।  

Plane Geometry

समतल ज्यामिति समतल आकृतियों से संबंधित है जिन्हें कागज के एक टुकड़े पर खींचा जा सकता है। इनमें दो आयामों की रेखाएं, वृत्त और त्रिभुज शामिल हैं। समतल ज्यामिति को द्वि-आयामी ज्यामिति के रूप में भी जाना जाता है। सभी द्वि-विमीय आकृतियों में केवल दो माप होते हैं जैसे लंबाई और चौड़ाई। यह आकृतियों की गहराई से संबंधित नहीं है। समतल आकृतियों के कुछ उदाहरण वर्ग, त्रिभुज, आयत, वृत्त आदि हैं। यहाँ, समतल ज्यामिति में कुछ महत्वपूर्ण शब्दावली की व्याख्या की गई है।

बिंदु

एक बिंदु एक विमान पर एक सटीक स्थान या स्थान है। एक बिंदु आमतौर पर उनका प्रतिनिधित्व करता है। यह समझना महत्वपूर्ण है कि एक बिंदु कोई चीज नहीं है, बल्कि एक जगह है। इसके अलावा, ध्यान दें कि एक बिंदु का कोई आयाम नहीं है; अधिमानतः, इसकी एकमात्र स्थिति है।

लाइन

रेखा सीधी है (कोई वक्र नहीं), जिसकी कोई मोटाई नहीं है और बिना अंत (असीम) दोनों दिशाओं में फैली हुई है। यह ध्यान रखना महत्वपूर्ण है कि यह एक रेखा बनाने के लिए अनंत बिंदुओं का संयोजन है। ज्यामिति में, हमारे पास एक क्षैतिज रेखा और लंबवत रेखा होती है जो क्रमशः x-अक्ष और y-अक्ष होती है।

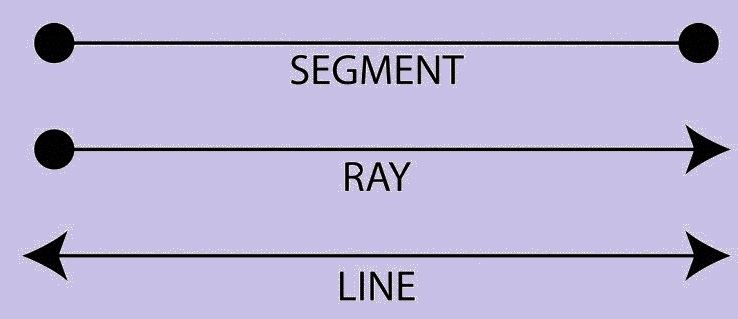
ज्यामिति में रेखाएं

• रेखा खंड - यदि किसी रेखा का एक प्रारंभिक और एक अंत बिंदु है तो उसे रेखा खंड कहा जाता है।
• किरण - यदि किसी रेखा का आरंभिक बिंदु हो और उसका कोई अंत बिंदु न हो तो किरण कहलाती है।

उदा. सूरज की किरणे

Angles in Geometry

तलीय ज्यामिति में, एक कोण दो किरणों द्वारा बनाई गई आकृति है, जिसे कोण की भुजाएँ कहा जाता है, जो एक सामान्य समापन बिंदु को साझा करती है, जिसे कोण का शीर्ष कहा जाता है।

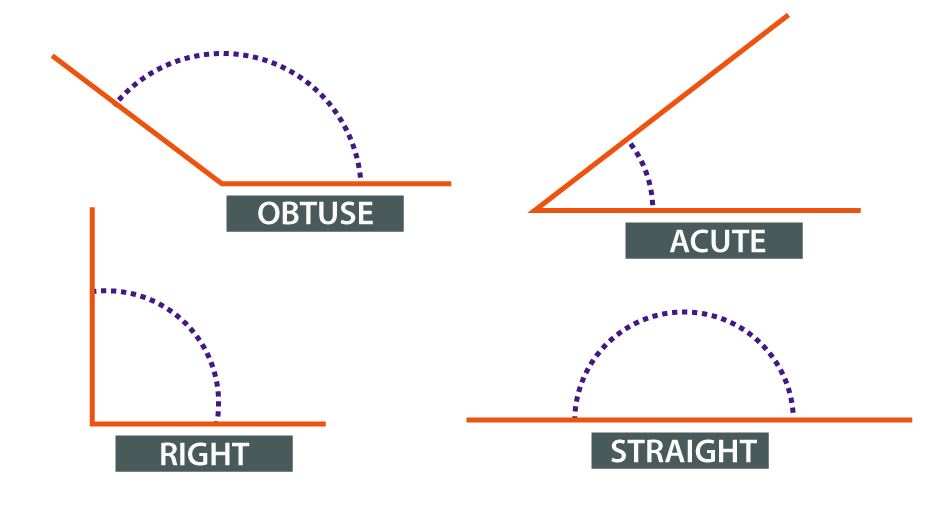
कोण के प्रकार

• न्यून कोण - एक न्यून कोण (या तीव्र कोण) एक समकोण अर्थात समकोण से छोटा कोण होता है। यह 0 - 90 डिग्री के बीच हो सकता है।
• अधिक कोण - एक अधिक कोण 90 डिग्री से अधिक लेकिन 180 डिग्री से कम होता है।
• समकोण - 90 डिग्री का कोण।
• सीधा कोण - 180 डिग्री का कोण एक सीधा कोण होता है, यानी एक सीधी रेखा से बनने वाला कोण 

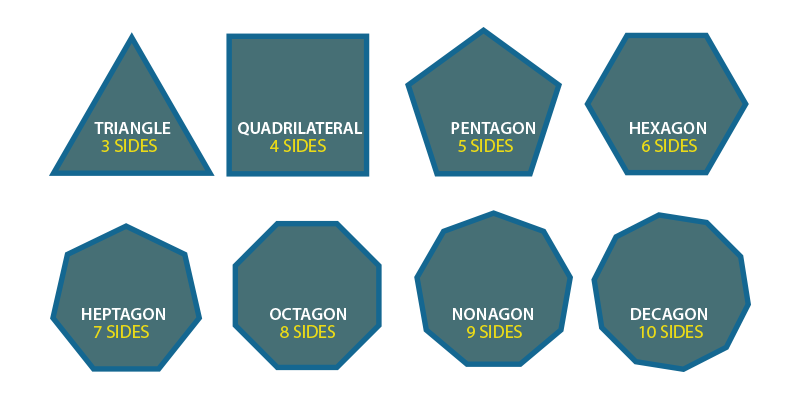
Polygons in Geometry

एक समतल आकृति जो एक बंद बहुभुज श्रृंखला या परिपथ बनाने के लिए एक लूप में बंद सीधी रेखा खंडों की एक परिमित श्रृंखला से घिरी होती है।

'पॉली' नाम कई को संदर्भित करता है। एक n-gon n भुजाओं वाला एक बहुभुज है; उदाहरण के लिए, एक त्रिभुज एक 3-गॉन बहुभुज है।

बहुभुज के आंतरिक कोणों के योग का सामान्य सूत्र:

बहुभुज के आंतरिक कोणों का योग =  (n - 2) × 180

(n−2)×180(n−2)×180(n−2)×180

Types of Polygon

The types of polygons are: 

• Triangles
• Quadrilaterals
• Pentagon
• Hexagon
• Heptagon
• Octagon
• Nonagon
• Decagon

 

Polygon type	Definition & Property	Types
(i) Triangle –	A 3-sided polygon whose sum of internal angles always sums to 180 degrees.	Equilateral Triangle – Has 3 equal sides and angles. Isosceles triangle –  Has 2 equal sides and angles. Scalene triangle – Has all the 3 unequal sides and angles.
(ii) Quadrilateral	A 4-sided polygon with four edges and four vertices. Sum of internal angles is 360 degrees	Square – Has 4 equal sides and vertices which are at right angles. Rectangle – Has equal opposite sides and all angles are at right angles. Parallelogram – has two pairs of parallel sides. The opposite sides & opposite angles are equal in measure. Rhombus – Has all the four sides to be of equal length. However, they do not have its internal angle to be 90 degrees Trapezium – Has one pair of opposite sides to be parallel.
(iii) Pentagon	A plane figure with five straight sides and five angles	–
(iv) Hexagon	A plane figure with six straight sides and six angles	–
(v) Heptagon	A plane figure with seven sides and seven angles	–
(vi) Octagon	A plane figure with eight straight sides and eight angles.	–
(vii) Nonagon	A plane figure with nine straight sides and nine angles.	–
(viii) Decagon	A plane figure with ten straight sides and ten angles.	–

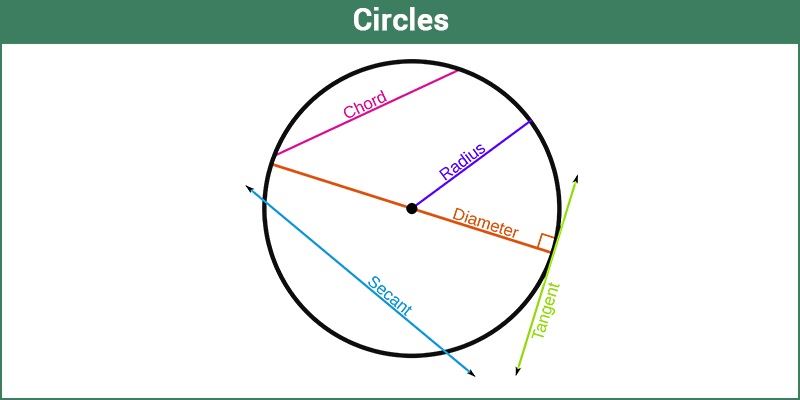
Circle in Geometry

एक वृत्त एक साधारण बंद आकृति है। एक निश्चित बिंदु से, जिसे केंद्र कहा जाता है, एक वृत्त के सभी बिंदु समान समान दूरी के होते हैं, अर्थात एक ऐसे बिंदु से वक्र का पता लगाया जाता है जो केंद्र से इसकी दूरी स्थिर रहता है।

समानता और सर्वांगसमता

• समरूपता - दो आकृतियों को समान कहा जाता है यदि उनका आकार समान हो या उनका कोण समान हो लेकिन उनका आकार समान न हो।
• सर्वांगसमता - दो आकृतियों को सर्वांगसम कहा जाता है यदि उनका आकार और आकार समान हो। इस प्रकार, वे पूरी तरह से बराबर हैं।

Solid Geometry

सॉलिड ज्योमेट्री क्यूब, प्रिज्म, सिलिंडर और गोले जैसी 3-आयामी वस्तुओं से संबंधित है। यह आकृति के तीन आयामों जैसे लंबाई, चौड़ाई और ऊंचाई से संबंधित है। लेकिन कुछ ठोस ठोसों के फलक नहीं होते (जैसे गोला)।

ठोस ज्यामिति यूक्लिडियन अंतरिक्ष में तीन आयामों का अध्ययन है। हमारे चारों ओर जो वस्तुएँ हैं वे त्रि-आयामी हैं। सभी त्रि-आयामी आकार 2डी आकृतियों के रोटेशन ऑपरेशन से प्राप्त होते हैं। 3D आकृतियों की महत्वपूर्ण विशेषताएँ चेहरे, किनारे और शीर्ष हैं। यहां विभिन्न ज्यामितीय आकृतियों के लिए इन शब्दों को विस्तार से पढ़ें।

किनारों

एक किनारे को सीमा पर रेखा खंड के रूप में परिभाषित किया जाता है जो एक शीर्ष को दूसरे शीर्ष से जोड़ता है। इसका मतलब है कि यह एक कोने से दूसरे कोने को जोड़ता है। यह 3D आकृतियों का कंकाल बनाता है। दूसरे शब्दों में, इसे फलकों के रूप में परिभाषित किया जा सकता है, जो सीधी रेखा में मिलते हैं किनारे कहलाते हैं। विभिन्न ठोस आकृतियों के किनारों की सूची निम्नलिखित है:

Solid Shapes	No. of. Edges
Triangular Prism	9
Cube	12
Rectangular prism	12
Pentagonal Prism	15
Hexagonal Prism	18
Triangular Pyramid	6
Square Pyramid	8
Pentagonal Pyramid	10
Hexagonal Pyramid	12

चेहरे(Faces)

हम जानते हैं कि सभी ज्यामितीय आकृतियाँ समतल सतह से बनी होती हैं जिन्हें फलक कहते हैं। यह किनारों से घिरी एक सपाट सतह है। किसी भी त्रि-आयामी आकृतियों के लिए, चेहरा एक द्वि-आयामी आकृति होना चाहिए। विभिन्न ठोस आकृतियों के फलकों की संख्या की सूची नीचे दी गई है:

Solid Shapes	No. of. Faces
Triangular Prism	5
Cube	6
Rectangular prism	6
Pentagonal Prism	7
Hexagonal Prism	8
Triangular Pyramid	4
Square Pyramid	5
Pentagonal Pyramid	6
Hexagonal Pyramid	7

कोने

एक शीर्ष को उस बिंदु के रूप में परिभाषित किया जाता है जहां ठोस आकृति के किनारे एक दूसरे पर मिलते हैं। दूसरे शब्दों में, यह कहा जा सकता है कि, वह बिंदु जहाँ बहुभुज की आसन्न भुजाएँ मिलती हैं। शीर्ष वे कोने हैं जहां किनारे मिलते हैं। ज्यामिति में विभिन्न ठोस आकृतियों के शीर्षों की संख्या इस प्रकार है:

Solid Shapes	No. of. Vertices
Triangular Prism	6
Cube	8
Rectangular prism	8
Pentagonal Prism	10
Hexagonal Prism	12
Triangular Pyramid	4
Square Pyramid	5
Pentagonal Pyramid	6
Hexagonal Pyramid	7

Frequently Asked Questions of Geometry

ज्यामिति का उपयोग कैसे किया जाता है?

ज्यामिति का उपयोग विभिन्न आकृतियों और आकारों, जैसे वृत्त, वर्ग, घन, त्रिकोण, आदि के विन्यास और माप में किया जाता है।

सभी ज्यामिति अनुप्रयोग क्या हैं?

दैनिक जीवन में ज्यामिति का व्यापक उपयोग होता है। इसके प्रमुख अनुप्रयोग निर्माण के क्षेत्र में हैं, जैसे भवन, सड़कों, बांधों, पुलों आदि का निर्माण और सर्वेक्षण, मानचित्रण, नेविगेशन में भी। सॉफ्टवेयर उद्योगों में, इसका उपयोग ग्राफिक्स डिजाइनिंग, गेमिंग, एनिमेशन आदि में किया जाता है। चिकित्सा क्षेत्र में भी, सीटी स्कैनिंग और एमआरआई की ज्यामिति अवधारणाओं का उपयोग किया जाता है।

ज्यामिति क्यों महत्वपूर्ण है?

हमारे जीवन में, विभिन्न आकृतियों को समझने और क्षेत्रफल और आयतन के आधार पर उन्हें मापने के लिए ज्यामिति महत्वपूर्ण है।

ज्यामिति का क्या अर्थ है?

ज्यामिति का अर्थ है पृथ्वी का माप, जैसा कि यह प्राचीन ग्रीक शब्दों से लिया गया है, 'जियो' का अर्थ है पृथ्वी और 'मेट्रॉन' का अर्थ है माप। तो कोई भी वस्तु जो पृथ्वी पर मौजूद है उसका एक आकार होता है जिसे ज्यामिति द्वारा परिभाषित किया जाता है।